Let's rename
|
|
(2017 Feb blog post)
Home >
Blog menu >
This page suggesting
'imaginary numbers' be called
'perpendicular numbers'
! Note !
Some web-links or images or paragraphs
may be added/changed ---
if/when I re-visit this page.
|
INTRODUCTION : I remember in math classes that when I was introduced to 'imaginary numbers', I was influenced by their name to think of them as some kind of 'second class' numbers --- numbers that really do not exist --- some kind of 'ghost numbers'. Furthermore, 'imaginary numbers' were teamed up with (added to) 'real numbers' to give 'complex numbers'. That name 'complex number' was intimidating to me. It immediately gave the impression of a number that is too tough to deal with. No wonder so many people are put off by mathematics. Mathematicians themselves give 'off-putting' names to the concepts with which they deal. Who wants to spend a lot of effort dealing with 'complex numbers'? Their very name indicates that they will be a real chore to handle. And who wants to waste their time on 'imaginary numbers'? It sounds like they really do not amount to anything anyway. Their very names suggest that it is way more pleasurable to watch TV or go tailgate at a football game than to struggle with 'complex' numbers --- or waste time on 'imaginary' numbers. A (very) Little History Imaginary numbers came about around the 1400's and 1500's as humans tried to find all the roots (solutions) to quadratic equations --- of the form a * x^2 + b * x + c = 0 where a, b , and c are 'real' numbers and x is the unknown real number(s) to be found so that the left-hand-side evaluates to zero. In those days, in Italy, a human who thought he/she had the upper hand in finding solutions to equations like this would challenge another human in a public display of who could best the other. In these publicly acted out challenges, one person would pose a problem that the second one would be challenged to solve. And the second one would, in turn, offer problems that the first would be challenged to solve. It became a game of devising solutions to equations, but keeping those solutions secret in order to have the upper hand when participating in these challenges. But, just as with magician tricks, some people were motivated, for various reasons, to reveal (publish) the methods of solution to problems like these. The history books tell us that one of the first people to use 'imaginary' and 'complex' numbers as an aid in solving challenge problems like these was Rafael Bombelli (1526 - 1572). And Bombelli was building on equation solving methods that were developed, more or less secretly, by people born somewhat before him --- such as Gerolamo Cardano (1501 - 1576) and Niccolò Fontana Tartaglia (1500 - 1557) and Lodovico Ferrari (1522 - 1565). In later years, people like the Swiss Leonhard Euler (1707 - 1783) greatly expanded on the properties of imaginary and complex numbers --- partly by examining power series expansions of functions like the exponential function and the sine and cosine functions. Eventually, in the 1800's and 1900's, physicists and engineers discovered that imaginary numbers were not so imaginary after all. They could be used quite handily to describe what is going on in electric circuits and what is going on in atoms at the quantum mechanical level. So it seems that the time is much over-due to ditch names like 'imaginary number' and 'complex number' and use names that are (if not descriptive of the utility of these numbers) at least more neutral (less negative) in their expressiveness. Suggestion 1 I suggest that we rename 'imaginary' numbers to 'perpendicular' numbers. This comes from the fact that we humans have taken to thinking of 'imaginary' and 'real' numbers as being pairs of real numbers plotted on a 'complex plane' --- with the 'real' numbers plotted horizontally (along an x-axis) and with the 'imaginary' numbers plotted vertically (along a y-axis). Hence the 'imaginary' numbers are, in a sense, perpendicular to the 'real' numbers. 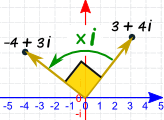In fact, when you multiply a 'real' number by the 'imaginary' number 'i', the imaginary number 'i' essentially rotates the real number 90 degrees in the complex plane so that the 'real' number lies on the y-axis instead of the x-axis. 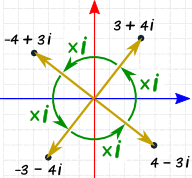Further, when you multiply the 'imaginary' number 'i' by the 'imaginary' number 'i', the imaginary number 'i' essentially rotates 90 degrees in the complex plane and becomes the 'real' number -1, which lies on the x-axis instead of on the y-axis. And, more generally, when you multiply a 'complex' number, a + b*i, by the 'imaginary' number 'i', the imaginary number 'i' essentially rotates the complex number 90 degrees in the complex plane so that the 'complex' number, a + b*i, becomes the complex number, -b + a*i. Hence we have plenty of reasons to call the 'imaginary' number 'i' a 'perpendicular' number. Note that 'imaginary' is 5 syllables and 'perpendicular' is 5 syllables --- a tie. For an even shorter name, how about 'right' number for 'imaginary' number --- as in 'right angle'? Some others to consider: 'rectified' number or 'vertical' number or 'erect' number or 'upright' number or ... Suggestion 2 Note that if we are going to do away with the name 'imaginary', we should also do something about that name 'real' --- because if we continue to use the name 'real', this implies that a 'perpendicular' number is not real. Since 'real' numbers are actually an extension of the 'rational' numbers by including all the limits of sequences of rational numbers, a name like 'extended-rational' numbers or 'extra-rational' numbers would be fairly descriptive without using 'emotionally discriminatory' names. However, those names are rather long --- so I suggest using a name like 'limit' numbers (or, even shorter, 'cut' numbers --- after Dedekind cut), in place of 'real' numbers. Suggestion 3 I suggest that we rename 'complex' numbers to 'compound' numbers. This would get rid of the negative connotation suggested by 'complex' --- and yet indicate that these numbers are composed of a combination of two types of numbers --- 'perpendicular' numbers and 'limit' numbers. In fact, I would suggest 'combination' numbers instead of 'complex' numbers --- but 'compound' number is shorter than 'combination' number. (Maybe 'pair' number? --- even shorter.) Note that the 'complex plane' would become the 'compound plane'. CONCLUSION So ... how about it, mathematicians out there ... on Earth? Let's all agree to replace the negatively-biased terms
with the less-negative terms
FOR FURTHER INFORMATION : For further information on these math-naming issues, here are some links to WEB SEARCHES on keywords related to this topic. After the search window appears with an intial page of 'hits', you can change or add keywords to hone the search to what you are looking for. |
|
Bottom of this page on blog topic
To return to a previously visited web page location, click on
the Back button of your web browser, a sufficient number of times.
OR, use the History-list option of your web browser.
< Go to Top of Page, above. >Or you can scroll up, to the top of this page. Page history:
Page was posted 2017 Feb 20.
|