-
Michel Rolle (1652 to 1719) was a French mathematician.
He is best known for Rolle's theorem (1691), and he deserves
to be known as the co-inventor in Europe of Gaussian elimination (1690).
-
Joseph Sauveur (1653 to 1716) was a French mathematician
and physicist. He was a professor of mathematics and in 1696
became a member of the French Academy of Sciences.
-
Pierre Varignon (1654 to 1742) was a French mathematician.
-
Jacob Bernoulli (1654 to 1705) - Law of Large Numbers
-
Jacques Bernoulli (1655 to 1705) - radius of curvature ~1692
-
Edmond Halley (ca. 1656 to 1742)
-
Charles Renee Reynaud (1656 to 1728)
-
Bernard de Fontanelle (1657 to 1757)
-
Jean Christophe Fatio (1659 to 1720)
-
David Gregory (1659 to 1708) was a Scottish mathematician
and astronomer. He was professor of mathematics at the University
of Edinburgh, Savilian Professor of Astronomy at the University
of Oxford, and a commentator on Isaac Newton's Principia.
He was a nephew of astronomer and mathematician James Gregory.
-
Marquis Guillaume de L'Hospital (1661 to 1704) Textbook on differential calculus ~1696
-
Louis Carre (1663 to 1711) was a French mathematician
and member of the French Academy of Sciences. He was the
author of one of the first books on integral calculus.
-
John Craig (1663 to 1731 ca. 1687) was a Scottish
mathematician and theologian.
-
Takebe Kenko (or Takebe Katahiro) (1664 to 1739)
-
Nicolas Fatio de Duiller (1664 to 1753)
-
Antoine Parent (1666 to 1716) was a French mathematician,
born at Paris and died there, who wrote in 1700 on
analytical geometry of three dimensions. His works were
collected and published in three volumes at Paris in 1713.
-
John Harris (ca. 1666 to 1719)
-
Abraham de Moivre (1667 to 1754)
-
Jean Bernoulli (Johann) (1667 to 1748)
-
Giovanni Girolamo Saccheri (1667 to 1733) was an Italian Jesuit
priest, scholastic philosopher, and mathematician.
-
Luigi Guido Grandi (1671 to 1742) was an Italian monk,
priest, philosopher, mathematician, and engineer.
-
George Cheyne (1671-1743) was a pioneering physician,
early proto-psychologist, philosopher and mathematician.
-
John Keill (1671 to 1721) was born in Edinburgh,
Scotland, and was primarily a mathematician and a disciple
of Isaac Newton. He studied at Edinburgh University,
under David Gregory, and obtained his bachelors degree
in 1692 with a distinction in physics and mathematics.
-
William Jones (1675 to 1749) was a Welsh mathematician,
most noted for his proposal for the use of the Greek letter pi
to represent the ratio of the circumference of a circle to
its diameter. He was a close friend of Sir Isaac Newton and
Sir Edmund Halley. In November, 1711 he became a Fellow of
the Royal Society, and was later its Vice-President.
-
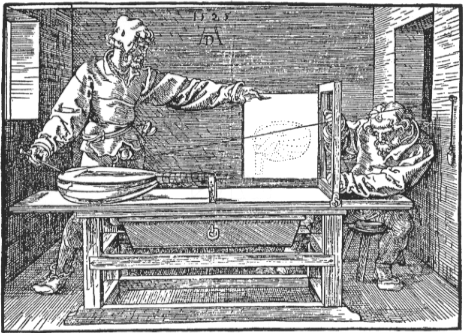
Humphry Ditton (1675 to 1715) was an English mathematician.
He studied theology, but on the death of his father, he devoted
himself to the study of mathematics. Through the influence of
Isaac Newton he was elected mathematical master in Christ's Hospital.
He did work on perspective.
-
Jacopo Riccati (1676 to 1754) was an Italian mathematician,
born in Venice. He is now remembered for the Riccati equation.
-
Antonio Schinella Conti (1677 to 1749) was an Italian
historian, mathematician, philosopher and physicist. He was
known as Abbé Conti (in Italian, Abate Conti) and is famous
for having been the intermediary, in England in 1715-16,
in the Leibniz-Newton calculus controversy.
-
Jacques Cassini (1677 to 1756) was a French astronomer,
son of the famous Italian astronomer Giovanni Domenico Cassini.
-
Pierre Rémond de Montmort (1678 to 1719) was a French mathematician.
De Montmort is known for his book on probability and games of chance.
Another of de Montmort's interests was the subject of finite differences.
-
Charles Hayes (1678-1760) was an English mathematician
and chronologist, author of an early book on the method of fluxions.
-
Jakob Hermann (1678 to 1733) was a mathematician who
worked on problems in classical mechanics. He appears to
have been the first to show that the Laplace-Runge-Lenz
vector is a constant of motion for particles acted upon
by an inverse-square central force. He received his
initial training from Jacob Bernoulli and was a distant
relative of Leonhard Euler.
-
Ephraim Chambers (ca. 1680 to 1740) Wrote 'Cyclopaedia'.
-
John Colson (1680 to 1760) Translated several of Newton's
works into English.
-
Gabriele Manfredi (1681 to 1761) was an Italian mathematician who
undertook important work in the field of calculus.
-
Roger Cotes (1682 to 1716) was an English mathematician,
known for working closely with Isaac Newton by proofreading
the second edition of his famous book, the Principia, before
publication. He also invented the quadrature formulas known
as Newton-Cotes formulas and first introduced what is known
today as Euler's formula. He was the first Plumian Professor
at Cambridge University from 1707 until his death.
-
Count Giulio Carlo di Fagnano (1682 to 1766) was an Italian mathematician.
He was probably the first to direct attention to the theory of elliptic integrals.
-
Amédée-François Frézier (1682 to 1773)
-
Savin (ca. 1701) (need info and link)
-
Guisnee (ca. 1705) (need info and link)
-
Chamberlayne (ca. 1718) (need info and link)
-
Burkhardt (ca. 1721) (need info and link)
-
Bragelonge (ca. 1730) (need info and link)
-
Brook Taylor (1685 to 1731), an English mathematician, coined the
phrase "vanishing point". His treatise 'Linear Perspective' (1715) expounded
the principle of vanishing points and was of value to artists.
This is the same Taylor who originated Taylor's theorem, a formula important
in differential calculus, which relates a function to its derivatives by
means of a power series.
-
Nicolaus I Bernoulli (1687 to 1759)
-
Robert Simson (1687 to 1768 ca. 1756) A Scottish
mathematician and professor of mathematics at the
University of Glasgow. In 1756, appeared, both in Latin
and in English, the first edition of his Euclid's 'Elements'.
This work, which contained only the first six and the
eleventh and twelfth books, and to which, in its English
version, he added the Data in 1762, was for long the
standard text of Euclid in England.
-
Christlieb von Clausberg (1689 to 1751) Died in Copenhagen. (need more info and link)
-
Christian Goldbach (1690 to 1764) conjectured that every even number
above two is the sum of two primes. Although 'The Goldbach Conjecture' has
been verified (as of 2008) up to a very large number, general proof is still
elusive.
-
Heinrich? Kuhn (1690? to 1769?)
A teacher in Danzig. In 1750, was
the first to give the square root of minus one a
geometric picture, analogous to the geometric interpretation
of the negative reals. (need more info and a link)
Mentioned in 'A History of Mathematics' by Cajori.
-
James Stirling (1692 to 1770) was a Scottish mathematician.
The Stirling numbers, Stirling permutations, and Stirling's
approximation are named after him. He also proved the correctness
of Isaac Newton's classification of cubics
-
Henry Pemberton (1694 to 1771) was an English physician
and man of letters. He became Gresham Professor of Physic,
and edited the third edition of Principia Mathematica.
-
Voltaire (1694 to 1778)
-
Nicolaus II Bernoulli (1695 to 1726)
-
Henri Pitot (1695 to 1771) was a French hydraulic engineer
and the inventor of the pitot tube. The
Pitot theorem
of plane geometry is named after him.
-
Colin MacLaurin (1698 to 1746) was a Scottish mathematician.
The Maclaurin series, a special case of the Taylor series,
is named after him.
-
George Campbell (ca. 1700 to 1766) Involved in a dispute
with
Colin MacLaurin (1698 - 1746) over complex roots.
-
Samuel Klingenstierna (1698 to 1765) Swedish mathematician
-
Maupertuis (1698 to 1759) Often credited with having invented
the
principle of least action.
-
Pierre Bonger (1698 to 1758) (need more info and link)
-
Daniel Bernoulli (1700 to 1782)
-
William Braikenridge (also Brakenridge) (1700? to 1762) was
a Scottish mathematician and cleric, a Fellow of the Royal Society
from 1752.In geometry the
Braikenridge-Maclaurin theorem was independently discovered
by Colin Maclaurin. It occasioned a priority dispute after
Braikenridge published it in 1733.
-
Edmund Stone (ca. 1700 to 1768) Son of a gardener of the
Duke of Argyll.
Self-taught.
-
Charles Marie de la Condamine (1701 to 1774)
-
Thomas Bayes (1701 to 1761) An English
mathematician and Presbyterian minister, known for
having formulated a specific case of the theorem that
bears his name:
Bayes's theorem. His friend Richard Price edited
and presented this work in 1763, after Bayes' death,
as 'An Essay towards solving a Problem in the Doctrine of
Chances'.
-
Georg Wolfgang Krafft (1701 to 1754) When Euler became
the professor of mathematics in St. Petersburg in 1733, Krafft
took over Euler's previous position, that of professor of
physics.
-
Gabriel Cramer (1704 to 1752)
Swiss mathematician --- namesake of
Cramer's rule.
-
Louis Goudin (1704 to 1760) A French
astronomer and member of the French Academy of Sciences.
He worked in Peru, Spain, Portugal and France.
-
Johann Andreas Segner (1704 to 1777) Was a Hungarian-born
scientist. He was born in the Kingdom of Hungary, in the
former Hungarian capital city of Pozsony (today Bratislava).
In 1735, Segner became the first professor of mathematics
at the University of Göttingen, a position created for him.
One of the best-known scientists of his age, Segner was a
member of the academies of Berlin, London, and Saint Petersburg.
Segner produced the first proof of Descartes' rule of signs.
He was the first scientist to use the reactive force of water
and constructed the first water-jet, the Segner wheel,
which resembles one type of modern lawn sprinkler.
Historians of science remember him as the father of the
water turbine.
-
Jean Castillon [aka Giovanni Salvemini] (1704-1791)
Was as an Italian mathematician and astronomer. In 1745,
he was elected to the Royal Society. In 1765, Frederick
the Great appointed him 'Astronomer Royal' of the
Observatory of Berlin. Succeeding Joseph-Louis Lagrange,
he was appointed Director of the Mathematics Section of
the Berlin Academy, a role he held until his death.
He studied conic sections, cubic equations and problems
of artillery. Among his latest publications mathematics
note He is also known for the "Castillon's problem".
-
Leonhard Euler (1707 to 1783) - super prolific mathematician.
-
solved the 7 bridges of Konigsberg problem ---
led to graph theory
-
V + F = E + 2 --- the formula connecting the
vertices, faces, and edges of a solid plyhedron.
-
The number 'e' is such that the gradient of
y=e^x is equal to itself.
-
e^(i x pi) = -1
-
Vincenzo Riccati (1707 to 1775)
-
Giordano Riccati (1709 to 1790)
-
Eustachio Zanotti (1709-1782) Was a noted astronomer
and mathematician and was the son of Giampietro Zanotti,
an Italian painter and art historian. (need a better link)
-
Thomas Simpson (1710 to 1761) Wrote popular textbooks,
including works on 'fluxions'.
-
Patrick_Murdoch (ca. 1710? to 1774) Part of Murdoch's 1746
'Newtoni genesis curvarum per umbras' (Newton's generation
of curves by shadows) deals with perspective.
-
François Jacquier (1711 to 1788) A French priest.
In 1739-42, François Jacquier and another French priest,
Thomas LeSeur (17xx? to 17xx?), produced, with the
assistance of
Jean-Louis Calandrini (1703-1758), an extensively
annotated version of the
1726 3rd edition of Newton's 'Principia'. Sometimes this
is referred to as the 'Jesuit edition'. It was much used, and
reprinted more than once in Scotland during the 19th century.
-
David Hume (1711 to 1776) Scottish philosopher,
historian, economist.
-
Johann Samuel König (1712 to 1757) Had disagreements
with Euler on the principle of least action.
-
Christian Ehrenfried Eschenbach (1712-1788)
belongs to the forerunners of scholars of legal medicine in Germany.
As a principal re-elected 11 times and dean of the medical faculty
at Rostock University, he defended academic positions in difficult
times. His bibliography comprises numerous text books, e.g. on surgery,
anatomy, pathology and obstetrics as well as various fields of mathematics.
-
Alexis Claude Clairaut (1713 to 1765) See
Clairaut's theorem and
Clairaut's equation and
Clairaut's relation.
-
Jean Paul de Gua (1713 to 1785) A French mathematician
who published in 1740 a work on analytical geometry in
which he applied it, without the aid of differential calculus,
to find the tangents, asymptotes, and various singular points
of an algebraic curve.
-
Denis Diderot (1713 to 1784) Best known for
serving as co-founder, chief editor, and contributor to
the Encyclopédie along with Jean le Rond d'Alembert (below).
First volume was published in 1751.
-
Cesar Francois Cassini (1714 to 1784)
French astronomer-surveyor-cartographer.
-
Arima Yoriyuki (1714 to 1783) Japanese mathematician.
In 1766, he found the a rational approximation of pi,
correct to 29 digits --- the ratio of two 15 digit integers.
-
Barmann (ca. 1745) (more info and link needed)
-
Jean d'Alembert (1717 to 1783) French mathematician,
mechanician, physicist, philosopher, and music theorist.
D'Alembert's formula for obtaining solutions to the wav
equation is named after him. The wave equation is sometimes
referred to as D'Alembert's equation.
-
Francesco Riccati (1718 to 1791) A son of Jacopo Ricatti (above).
Italian architect. (more info and better link needed)
-
Maria Gaetana Agnesi (1718 to 1789) An Italian
mathematician and philosopher. She is credited with
writing the first book discussing both differential and
integral calculus and was an honorary member of the
faculty at the University of Bologna.
-
Matthew Stewart (1719 to 1785) Published
Stewart's theorem in 1746.
-
Abraham Gotthelf Kastner (1719 to 1800) German mathematician
known for his textbooks.
-
John Landen (1719 to 1790 ca. 1771) An English
mathematician. Landen's capital discovery is that of the
Landen's transformation for the expression of the arc
of an hyperbola in terms of two elliptic arcs. His researches
on elliptic functions are of considerable elegance, but
their great merit lies in the stimulating effect which
they had on later mathematicians. He also showed that the
roots of a cubic equation can be derived by means of
the infinitesimal calculus. He lived a very retired life,
and saw little or nothing of society. When he did mingle
in it, his dogmatism and pugnacity caused him to be
generally shunned.
-
Fridericus Guilielmus De Oppel (1720 to 1769) Wrote
'Analysis Triangulorum' (1746). (need more info and link)
-
Joseph Torelli (1721 to 1781) was an Italian mathematician.
His edition of the collected works of Archimedes was printed
at Oxford in 1792. The preparation of this work was a
labour performed, among many other pursuits, during most of his life.
-
Ravelli (ca. 1751) (need more info and a link)
-
John Lawson (1723 to 1779) An English mathematician.
Published some works on tangencies.
-
Jean-Étienne Montucla (1725 to 1799) Wrote a history of
math. The first part was published in 1758.
-
Johann Heinrich Lambert (1728 to 1777) A Swiss
mathematician, physicist, philosopher and astronomer.
He is best known for proving the irrationality of pi.
-
Fredric Mallet (1728 to 1797) Was one of
Klingenstierna's (above, 1698) most devoted students.
Sorted through Klingenstierna's manuscripts for
eventual publication. (need a better link)
-
Charles Bossut (1730 to 1814) Was a French mathematician.
His works include 'Traité élémentaire d'hydrodynamique' in 1771,
'Traité élémentaire de méchanique statique' in 1772,
'Cours de mathématiques' in 1781, and 'Histoire générale
des mathématiques' in 1810.
-
Étienne Bezout (1730 to 1783) A French
mathematician. Wrote 'Théorie générale des équations
algébriques', published at Paris in 1779, which,
in particular, contained much new and valuable matter
on the theory of elimination and symmetrical functions
of the roots of an equation. He used determinants in
a paper in the 'Histoire de l'académie royale', 1764,
but did not treat the general theory.
-
Martin Johan Wallenius (1731 to 1773) All five squarable
lunes
were given in a dissertation by Martin Johan Wallenius in 1766.
(need a better link)
-
Girolamo Saladini (1731-1813) Saladini was a
student of Vincenzo Riccati (above), and was a co-author
with Riccati of the two volume book 'Institutiones Analyticae'
(Vol 1, 1765; Vol 2, 1767) which contains the formulas for
the addition and subtraction of hyperbolic functions
as well as other, now standard, formulas analogous to
those for the circular (sin, cos) functions. They also computed
the derivatives of sinh x and cosh x. (need a better link)
-
Gian Francesco Malfatti (1731 to 1807) was an Italian
mathematician. He studied in Bologna where his mentors
included Vincenzo Riccati, F. M. Zanotti and G. Manfredi.
Malfatti posed the problem of carving three circular columns
out of a triangular block of marble, using as much of
the marble as possible, and conjectured that three
mutually-tangent circles inscribed within the triangle
would provide the optimal solution. These tangent circles
are now known as Malfatti circles after his work, despite
the earlier work of Japanese mathematician Ajima Naonobu
and of his countryman Gilio di Cecco da Montepulciano on
the same problem --- and despite the fact that the conjecture
was later proven false. Several triangle centers derived
from these circles are also named after both Ajima and
Malfatti. Additional topics in Malfatti's research
concerned quintic equations, and the property of the
lemniscate of Bernoulli that a ball rolling down an
arc of the lemniscate, under the influence of gravity,
will take the same time to traverse it as a ball rolling down
a straight line segment connecting the endpoints of the arc.
-
Francois Daviet de Foncenex (1734 to 1799) In 1759, he attempted a proof of
the fundamenatal theorem of algebra --- as did Euler in 1749,
Lagrange in 1772, and Laplace in 1795. (need a better link)
-
Achille_Pierre Dionis du Sejour (1734 to 1794)
was a French astronomer and mathematician. He wrote on
algebraic curves as well as on astronomy (planets and comets).
-
William Wales (1734? to 1798) Made astronical
observations and calculations on the 2nd voyage of Captain
James Cook.
-
Alexandre-Théophile Vandermonde (1735 to 1796)
A French musician (violinist), mathematician and chemist
who worked with Bézout and Lavoisier. His name is now
principally associated with determinant theory in mathematics.
-
Joseph Louis Lagrange (1736 to 1813) An Italian
mathematician and astronomer. He made significant
contributions to all fields of analysis, number theory,
and both classical and celestial mechanics. In 1766,
Lagrange succeeded Euler as the director of mathematics
at the Prussian Academy of Sciences in Berlin, Prussia,
where he stayed for over twenty years.
-
Edward Waring (1736 to 1798) An English mathematician who
was elected in 1760 as
Lucasian Professor of Mathematics at Cambridge,
holding the chair until his death. In 1762, he published
the full 'Miscellanea Analytica', mainly devoted to the
theory of numbers and algebraic equations. See
Waring's (number theory) problem and
Waring's prime number conjecture.
-
Erland Samuel Bring (1736 to 1798) was a Swedish
mathematician. At Lund University, he wrote eight volumes
of mathematical work in the fields of algebra, geometry,
analysis and astronomy, including 'Meletemata quaedam
mathematematica circa transformationem aequationum
algebraicarum' (1786). Bring developed a transformation
to simplify a quintic equation to the form x^5 + px + q = 0.
-
Jacques Antoine Joseph Cousin (1739 to 1800)
Wrote 'Lecons de Calcul Differentiel et de Calcul Integral'
(1777). His main position was as professor for mathematics
and experimental physics at the College Royale, which he
held from 1769 until his death. (need a better link)
-
Anders Johan Lexell (1740 to 1784)
was a Finnish-Swedish astronomer, mathematician, and
physicist who spent most of his life in Russia.
Lexell made important discoveries in
polygonometry and celestial mechanics. He contributed
to spherical trigonometry with new and interesting solutions,
which he took as a basis for his research of comet and
planet motion. His name was given to a theorem of
spherical triangles. Lexell was one of the most prolific
members of the Russian Academy of Sciences at that time,
having published 66 papers in 16 years of his work there.
In later life (circa 1783), Lexell became very attached to
Leonhard Euler, who lost his sight in his last years but
continued working using his elder son Johann Euler to read
for him. Lexell helped Leonhard Euler greatly, especially
in applying mathematics to physics and astronomy. He helped
Euler to write calculations and prepare papers.
-
Stanislaus Wydra (1741 to 1804) was a professor at
Prague University. He wrote an 88 page book titled
'Elementa Calculi Differentialis et Integralis' (1783).
He was a
pupil, and later biographer, of
Joseph Stepling. (Wydra/Vydra needs a better link)
-
Carl Hindenburg (1741 to 1808) was a German
mathematician born in Dresden. His work centered
mostly on combinatorics and probability.
Hindenburg co-founded the first German mathematical
journals. Between 1780 and 1800, he was involved at
different times with the publishing of four different
journals all relating to mathematics and its applications.
One of Hindenberg's best students, according to Donald
Knuth, is Heinrich August Rothe. Another student,
Johann Karl Burckhardt, published the book 'Theorie der
Kettenbrüche' after being encouraged by Hindenberg to
work on continued fractions. He also influenced
Christian Kramp's work in combinatorics.
-
Antonio Cagnoli (1743 to 1816) was an Italian
astronomer, mathematician and diplomat. He worked in
Paris and Verona. He set up an observatory in Verona ---
which was
damaged by Bonaparte's cannons, but Bonaparte
made amends with money and the gift a very accurate clock.
-
Marie Jean Antoine Nicolas de Caritat, marquis de Condorcet
(1743 to 1794) was a French philosopher, mathematician,
and early political scientist whose Condorcet method
in voting tally selects the candidate who would beat
each of the other candidates in a run-off election.
Condorcet was one of the first to systematically
apply mathematics in the social sciences. In 1786, Condorcet
worked on ideas for the differential and integral calculus,
giving a new treatment of infinitesimals - a work
which was never printed.
-
Caspar Wessel (1745 to 1818) A Norwegian-Danish
mathematician and cartographer. In 1799, Wessel was
the first person to describe the geometrical interpretation
of complex numbers as points in the complex plane.
-
Gaspard Monge (1746 to 1818) Was a French mathematician,
the inventor of descriptive geometry (the mathematical
basis of technical drawing), and the father of differential
geometry. During the French Revolution he served as the
Minister of the Marine, and was involved in the reform
of the French educational system, helping to found the
École Polytechnique.
-
Reuben Burrow (1747 to 1792) An English mathematician
and orientalist. Initially a teacher, he was later appointed
astronomer-royal at the Royal Greenwich Observatory.
He later conducted research in India, becoming one of the
first members of the Asiatic Society. He was also interested
in ancient geometry, as he has proved by his book on
Apollonius: 'A Restitution of the Geometrical Treatise of
Apollonius Pergæus on Inclinations' (1779), and was
curious to investigate the mathematical treatises in
ancient Hindu and other Oriental literature. He later
published 'Hindoo Knowledge of the Binomial Theorem'.
-
Jean Dominque IV Cassini (1748 to 1845) French astronomer.
-
D'Amondans Charles de Tinseau (1748 to 1822)
Graduated as a military engineer in 1771 and later became
a mathematician after becoming a student of
Monge (above).
-
??? Rowing (ca. 1770) (need more info and link)
-
Pierre Simon de Laplace (1749 to 1827) A French
mathematician and astronomer whose work was pivotal
to the development of mathematical astronomy and statistics.
He summarized and extended the work of his predecessors
in his five-volume 'Mécanique Céleste' (Celestial Mechanics)
(1799-1825). This work translated the geometric study of
classical mechanics to one based on calculus, opening up
a broader range of problems. In statistics, the Bayesian
interpretation of probability was developed mainly by Laplace.
In France, the normal distribution is called the Laplacian
distribution. (In Germany, it is called the Gaussian
distribution.)
-
Lorenzo Mascheroni (1750 to 1800) was an
Italian mathematician. In his 'Geometria del Compasso'
(1797), he proved that any geometrical construction,
which can be done with compass and straightedge,
can also be done with compasses alone. However, the
priority for this result (now known as the Mohr-Mascheroni
theorem) belongs to the Dane Georg Mohr, who had
previously published a proof in 1672. In his
'Adnotationes ad calculum integrale Euleri' (1790),
he published a calculation of what is now known as
the Euler-Mascheroni constant, usually denoted as gamma.
-
Simon Antoine Jean L'Huilier (1750 to 1840)
was a Swiss mathematician of French Hugenot descent.
He is known for his work in mathematical analysis and
topology, and in particular the generalization of
Euler's formula for planar graphs.
-
Adrien-Marie Legendre (1752 to 1833) A French mathematician.
Legendre polynomials and Legendre transformation are named
after him. Legendre is known as the author of 'Éléments de
géométrie' which was published in 1794 and was the leading
elementary text on the topic for around 100 years. This
text greatly rearranged and simplified many of the propositions
from Euclid's Elements to create a more effective textbook.
-
Lazar Nicolas Carnot (1753 to 1823) was a French politician,
engineer, and mathematician. The Borda-Carnot equation of
fluid dynamics and Carnot's theorem in plane geometry
are named after him.
-
Captain William Lambton (1753 to 1823) was a British
soldier, surveyor, and geographer. He was involved in
surveying the boundary between Canada and the United States.
He also did surveying in India.
-
Jean Baptiste Meusnier (1754 to 1793) A French
mathematician, engineer and Revolutionary general.
He is best known for
Meusnier's theorem on the curvature of surfaces.
He also discovered the
helicoid. He worked with Lavoisier on the
decomposition of water and the evolution of hydrogen.
-
Jurij Vega (1754 to 1802) was a Slovene mathematician,
physicist and artillery officer. Vega published a series of
books of logarithm tables. His major work was 'Thesaurus
Logarithmorum Completus' (Treasury of all Logarithms)
that was first published 1794. Over the years, Vega wrote
a four volume textbook 'Vorlesungen über die Mathematik'
(Lectures about Mathematics). Volume I appeared in 1782
when he was 28 years old, Volume II in 1784, Volume III
in 1788 and Volume IV in 1800. His textbooks also contain
interesting tables: for instance, in Volume II one can
find closed form expressions for sines of multiples of
3 degrees, written in a form easy to work with. In 1789,
Vega achieved a world record when he calculated pi to 140
places, of which the first 126 were correct. Vega had improved
John Machin's formula from 1706.
-
Nicolas Fuss (1755 to 1826) was a Swiss mathematician,
living most of his life in Russia. He moved to Saint
Petersburg to serve as a mathematical assistant to
Leonhard Euler from 1773-1783, and remained there until
his death. He contributed to spherical trigonometry,
differential equations, the optics of microscopes and
telescopes, differential geometry, and actuarial science.
He also contributed to Euclidean geometry, including
the problem of Apollonius.
-
A. Giordano (ca. 1785) "... a Neapolitan lad A. Giordano,
who was only 16 but who had shewn marked mathematical ability
..." (need more info and a link)
-
Theodor von Schubert (1758 to 1825) became
a tutor of mathematics and astronomy.
In 1785, he became an assistant of the Russian Academy
of Sciences as a geographer, and by June 1789 he was
a full member. In 1803, he became head of the astronomical
observatory of the Academy. Wrote some texts on astronomy.
-
Louis Francois Antoine Arbogast (1759 to 1803) was a French
mathematician. He wrote on series and the derivatives
known by his name. His notion of using discontinuous functions
to integrate partial differential equations became important
in Cauchy's more rigorous approach to analysis. He conceived
the calculus as operational symbols. The formal algebraic
manipulation of series investigated by Lagrange and Laplace
in the 1770s has been put in the form of operator equalities
by Arbogast by 1800.
-
Paolo Ruffini (1765 to 1822) was an Italian mathematician and philosopher.
By 1788 he had earned university degrees in philosophy, medicine/surgery,
and mathematics. Among his work was an incomplete proof (Abel-Ruffini theorem)
that quintic (and higher-order) equations cannot be solved by radicals (1799),
and Ruffini's rule which is a quick method for polynomial division.
Ruffini also made contributions to group theory in addition to probability
and quadrature of the circle.
-
Sylvestre François Lacroix (1765 to 1843) was a French
mathematician. He displayed a particular talent for
mathematics, calculating the motions of the planets by
the age of 14. In 1793 he became examiner of the Artillery
Corps, replacing Pierre-Simon Laplace in the post. By 1794,
he was aiding his old instructor, Gaspard Monge, in creating
material for a course on descriptive geometry. In 1799, he
was appointed professor at the École Polytechnique. Lacroix
produced most of his texts for the sake of improving his
courses. During his career he produced a number of
important textbooks in mathematics. Translations of these
books into the English language were used in British
universities, and the books remained in circulation for
nearly 50 years.
-
Thomas Malthus (1766 to 1834), an English-born economist, used arithmetic
and geometric progressions to describe the growth of population.
Arithmetic progressions and
geometric progressions had been known since the time of the Greeks.
-
Joseph Fourier (1768 to 1830) was a French mathematician
and physicist. Best known for initiating the investigation of
Fourier series and their applications to problems of heat transfer
and vibrations. (Any wave form can be made by combining
sine and cosine functions.)
-
Jean Robert Argand (1768 to 1822) was a gifted amateur
mathematician. In 1806, while managing a bookstore in Paris,
he published the idea of geometrical interpretation of complex
numbers known as the Argand diagram. Argand is also renowned
for delivering a proof of the 'fundamental theorem of algebra'
in his 1814 work 'Réflexions sur la nouvelle théorie d'analyse'
(Reflections on the new theory of analysis). It was the first
complete and rigorous proof of the theorem, and was also the
first proof to generalize the fundamental theorem of algebra
to include polynomials with complex coefficients.
-
Jean Nicolas Pierre Hachette (1769 to 1834), French mathematician,
was born at Mézières, where his father was a bookseller. His labours
were chiefly in the field of descriptive geometry and 3 dimensions, with its
application to the arts and mechanical engineering. It was left
to him to develop the geometry of Monge, and to him also is due
in great measure the rapid advancement which France made soon
after the establishment of the École Polytechnique in the
construction of machinery.
-
Heinrich August Rothe (1773 to 1842) was a German
mathematician, a professor of mathematics at Erlangen.
The Rothe-Hagen identity, a summation formula for binomial
coefficients, appeared in Rothe's 1793 thesis. It is named
for him and for the later work of Johann Georg Hagen.
The same thesis also included a formula for computing the
Taylor series of an inverse function from the Taylor series
for the function itself, related to the Lagrange inversion
theorem. In the study of permutations, Rothe was the
first to define the inverse of a permutation, in 1800.
He developed a technique for visualizing permutations
now known as a Rothe diagram.
-
Nathaniel Bowditch (1773 to 1838) was an early
American mathematician remembered for his work on
ocean navigation. He is often credited as the founder
of modern maritime navigation. His book 'The New
American Practical Navigator', first published in 1802,
is still carried on board every commissioned U.S. Naval vessel.
-
Louis Poinsot (1777 to 1859) added two new regular solids
to the five Platonic solids and the two 'stellated'
regular solids pointed out by Kepler --- for a total of nine.
-
the five Platonic solids (tetrahedron, octahedron,
cube, dodecahedron, icosahedron)
-
small stellated dodecahedron - attributed to
Kepler and, before Kepler, to artist
Paolo Uccello (1397-1475)
-
great stellated dodecahedron - attributed to
Kepler and, before Kepler,
to artist Wenzel Jamnitzer (1508-1585).
-
great dodecahedron (found by Poinsot)
-
great icosahedron (found by Poinsot)
Augustin Cauchy (1789-1857 ; see below) proved that
these are the only regular solids.
-
Carl Friedrich Gauss (1777 to 1855) devised a method of constructing a
17-sided polygon using straight edge and compass only. Greek mathematicians
had been able to constrocuh polygons of 3 and 5 sides with straight edge and
compass only. Gauss wanted a 17-sided polygon on his grave, but the stonemason
refused because it would simply look like a circle.
Going well beyond this, Gauss showed that a regular n-sided polygon can be
so constructed if n is a Fermat prime (2^2^k + 1, for an integer k). The
next Fermat primes after 17 are 257 and 65,537. In 1832, F.J. Richelot,
who taught mathematics at the University of Konigsberg, showed how to construct
a 257-sided polygon.
In 1894, J. Hermes wrote out the construction of a regular 65,537 sided polygon.
It had taken him 10 years and took up 200 pages. 'Unfortunately, it is likely
to contain a mistake.'
Gauss proved the
'Fundamental Theorem of Algebra': A polynomial equation of
degree n has n roots, in the complex plane. The theorem provides an example
of where the theory of complex numbers is more complete than that of the real
numbers.
-
Christoph Bernoulli (1782 to 1863)
-
Charles Julien Brianchon (1783 to 1864) was a French mathematician
and chemist. He entered into the École Polytechnique in 1804
and studied under Monge, graduating first in his class in 1808,
after which he took up a career as a lieutenant in Napoleon's
artillery. Later, in 1818, Brianchon became a professor in the
Artillery School of the Royal Guard at Vincennes. Brianchon is
best known for his proof of
Brianchon's theorem (1810).
-
Friedrich Bessel (1784 to 1846)
-
Charles Xavier Thomas de Colmar (1785 to 1870), a Frenchman who served in the
French army, in 1820 produced the first really successful commercial calculating
machine. (See Schickard, Pascal, and Leibniz above.) By the 1860's, the machine
was commercially successful. Under different guises, it continued to be produced
for well over 100 years --- to around 1920? or 1960?
-
Claude Louis Marie Henri Navier (1785 to 1836)
-
Jean Victor Poncelet (1788 to 1867)
-
Augustin Cauchy (1789 to 1857) provided rigorous definitions of the
concept of continuity of curves and their derivatives. He put the
field of 'real and complex analysis' on firm ground.
-
Jean Francois Champollion (1790 to 1832)
-
Abel (ca 1824)
-
August Mobius (1790 to 1868) conceived of the Mobius strip, which has
just one edge and one surface.
-
George Everest (1790 to 1866)
-
Charles Babbage (1791 to 1871) designed a 'difference engine' and an
'analytic engine' --- motivated by his thought: "I am thinking that these
tables [logarithms] might be calculated by steam."
The 'difference engine' had a fairly precise task --- to calculate and print
out the values of certain functions. Known values of the required function
were entered and the machine then calculated other values (thus the 'difference').
The 'analytic engine' was like a modern computer, except that it worked
mechanically rather than electronically. It was programmable, in that it could
carry out any mathematical task. It could branch and it could loop.
The analytic engine was never actually built. Babbage kept changing his mind
about what he wanted and quarreled with everyone working with him. The British
government withdrew from the project in 1842. The secretary of the Royal Astronomical
Society wrote: "We got nothing for our 17,000 pounds but Mr. Babbage's grumblings.
We should at least have had a clever toy for our money."
-
Nicolai Lobachevsky (1792 to 1856) developed a system of geometry
in which Euclid's 5th postulate (on parallel lines) no longer holds.
(See Janos Bolyai.)
-
Ernst Weber (1795 to 1878)
-
Jakob Steiner (1796 to 1863)
-
Gustav Theodor Fechner (1801 to 1887)
-
Janos Bolyai (1802 to 1850) developed a system of geometry
in which Euclid's 5th postulate (on parallel lines) no longer holds.
(See Nicolai Lobachevsky.)
-
Neils Abel (1802 to 1829), a Norwegian, in 1821, showed that there is no
algebraic formula for the roots of the general quintic equation.
-
William Rowan Hamilton (1805 to 1865) developed quaternions, which can be
used to model positions in four dimensions.
-
Thomas Kirkman (1806 to 1895) posed a problem in combinatorics called
'Kirkman's schoolgirl problem'. Sudoku puzzles are an example of these
types of combinatoric problem.
-
Joseph Liouville (1809 to 1882), in 1844, constructed the first
transcendental numbers --- numbers that were not the solutions of algebraic
equations (composed of polynomials).
-
Benjamin Peirce (1809 to 1880)
-
Evariste Galois (1811 to 1832) developed a theory of groups of permutations
of solutions to polynomial equations which was used to show that, although
quadratic, cubic, and quartic equations had a general solution in the form of
an algegraic formula, quintic (and higher) equations do not have such a general
solution.
'Group theory' became a major area of mathematics. It has been extened to many
other structures besides permutations and is used in nuclear and quantum physics.
-
Johann Gustav Bernoulli (1811 to 1863)
-
Pierre Wantzel (1814 to 1848) - Constructions with straight edge and
compass only (like the 3 Greek problems of trisecting the angle, squaring the
circle, and doubling the cube) were shown to be equivalent to using the four
basic operations of arithmetic ( + - x / ) and taking square roots. The way was
then clear to show that the Greek problems were insoluble. If a problem
involves a length which cannot be built up from 1 by + , - , x , / , and squre
root, then it cannot be constructed and the problem cannot be solved.
-
George Boole (1815 to 1864) set up a system to codify logical argument
as a form of algebra. This is used in the design of computer circuitry.
-
Karl Wierstrass (1815 to 1897) is called, by some, "the father of
modern analysis". He put calculus on more solid ground by introducing
more rigor in definitions and proofs.
-
John Tyndall (1820 to 1893)
-
Hermann Ludwig Helmholz (1821 to 1894)
-
Charles Hermite (1822 to 1901) showed in 1873 that the number 'e' is
transcendental.
-
Francis Galton (1822 to 1911) develped the 'correlation coefficient'.
-
Jule Antoine Lissajous (1822 to 1880)
-
Bernhard Riemann (1826 to 1866) - The Riemann Hypothesis is a conjecture
about the zeros, in the complex plane, of an infinite series. If this hypothesis
can be proved to be true, it will provide the solution to many other unsolved
problems.
-
James Clerk Maxwell (1831 to 1879) devised a set of equations summarizing
the behavior of electricity and magnetism.
-
Richard Dedekind (1831 to 1916)
-
Alvan Graham Clark (1832 to 1897)
-
Charles Lutwidge Dodgson - alias Lewis Carroll (1832 to 1898) besides
writing 'Alice in Wonderland', was a mathematician who devised a paradox
in which a tortoise traps Achilles into an infinite regress of implication.
There is a story that the British Queen Victoria (1819-1901; reigned 1837-1901)
was so delighted by the Alice books that she asked Dodgson to send her his
next publication. She was surprised, and probably disappointed, to receive
'An Elementary Treatise on Determinants'.
-
Alexander Henry Rhind (1833 to 1863) acquired the Rhind
Papyrus. (See 'Ahmes', an Egyptian scribe, at the top of
this list.)
-
John William Strutt (Lord Rayleigh) (1842 to 1919)
-
Georg Cantor (1845 to 1918) proved that the rational numbers can be
counted. Developed many other results on countability or non-countability
('infinities') of number systems.
-
Arnold Buffum Chace (1845 to 1932)
-
Julius Plucker (1801 to 1868) was a German
mathematician and physicist. He made fundamental
contributions to the field of analytical geometry and
was a pioneer in the investigations of cathode rays
that led eventually to the discovery of the electron.
He also vastly extended the study of Lamé curves.
In 1865, Plücker invented what was known as 'line geometry'
in the nineteenth century. In 'projective geometry',
Plücker coordinates refer to a set of homogeneous
co-ordinates introduced initially to embed the set of
lines in three dimensions as a quadric in five dimensions.
-
Friedrich Ludwig Gottlobb Frege (1848 to 1925)
was a German mathematician, logician and philosopher.
He is considered to be one of the founders of modern
logic and made major contributions to the foundations
of mathematics.
-
Felix Klein (1849 to 1925) conceived of the Klein bottle --- a twisted
shape that has no inside or outside, and exists only in four dimensions.
It can be made by joining two Mobius strips edge to edge, in four dimensions.
-
Oliver Heaviside (1850 to 1925)
-
Sonia Kovalevsky (1850 to 1891)
-
Ferdinand von Lindemann (1852 to 1939) proved that pi is transcendental
--- that is, not a solution of an algebraic equation. This showed that the
ancient Greek problem of 'squaring the cirle' (with straight edge and
compass only) was impossible.
-
Elisha Scott Loomis (1852 to 1940) was an American teacher,
mathematician, genealogist, writer and engineer. Probably his
best-known work is his book 'The Pythagorean Theorem', in
which he collected, classified, and discussed more than
340 proofs.
-
Egraf Stepanovich Fedorov (1853 to 1919) showed that precisely 17
wallpaper patterns exist, where a wallpaper pattern is a regular arrangement
of shapes, repeated across a plane. If all possible combinations of translations,
rotations, and reflections are considered, there are essentially
17 different types of pattern.
-
Henri Poincare (1854 to 1912) was a founder of the field of topology.
It is said that "Topologists think that a doughnut is the same as a coffee cup."
Topologists are not content with objects in two or three dimensions.
They extend the definitions of topology into four or more dimensions.
-
Aleksandr Lyapunov (1857 to 1918) - the Central Limit Theorem - the mean
of a large enough sample is approximately normal --- that is, if enough data
is taken, the normal distribution can be used to calculate probabilities.
-
Giuseppe Peano (1858 to 1932) constructed a 'space-filling curve- ---
a curve which is continuous,
no breaks in it, which passes through every point of a square --- even though
a square, unlike a line, is two dimensional and has non-zero area.
-
Max Planck (1858 to 1947) - a quantum physicist
-
Florian Cajori (1859 to 1930) was an American
historian of mathematics.
-
D'Arcy Wentworth Thompson (1860 to 1948) was a
Scottish biologist, mathematician, and classics scholar.
A pioneering mathematical biologist, he is mainly
remembered as the author of the 1917 book 'On Growth and Form'.
The book pioneered the scientific explanation of morphogenesis,
the process by which patterns are formed in plants and animals.
-
David Eugene Smith (1860 to 1944) was an American
mathematician, educator, and editor. He became a professor
of mathematics at Teachers College, Columbia University
(1901) where he remained until his retirement in 1926.
Smith became president of the Mathematical Association of
America in 1920. He wrote a large number of publications of
various types: He was editor of the Bulletin of the
American Mathematical Society; contributed to other
mathematical journals; published a series of textbooks;
translated Felix Klein's 'Famous Problems of Geometry',
Fink's 'History of Mathematics', and the 'Treviso Arithmetic'.
He edited Augustus De Morgan's 'A Budget of Paradoxes' (1915)
and wrote several textbooks on teaching mathematics.
-
Alfred North Whitehead (1861 to 1947) was an English
mathematical logician and philosopher.
-
David Hilbert (1862 to 1943), like Peano, devised a space-filling curve.
In a famous speech in 1900, he identified a set of unsolved mathematical problems
to be attacked in the next century. The Riemann hypothesis and Goldbach's conjecture
were on his list and they were still unsolved as of 2008 --- over a century later.
To solve a Hilbert problem has become a high ambition for any mathematician.
-
Hermann Minkowski (1864 to 1909) was a
Lithuanian-German mathematician. He used geometrical methods
to solve problems in number theory, mathematical physics,
and the theory of relativity.
-
Jacques Hadamard (1865 to 1963), like Charles de la Vallee Poussin,
proved that the density of the prime numbers thins out in a logarithmic fashion.
-
Charles de la Vallee Poussin (1866 to 1962), like Jacques Hadamard, proved
that the density of the prime numbers thins out in a logarithmic fashion.
-
Theodore_Andrea_Cook (1867 to 1928) wrote
'The Curves of Life: Being an Account of Spiral Formations
and Their Application to Growth in Nature, to Science and
to Art: with the special reference to the manuscripts of
Leonardo da Vinci'(1914). According to Cook,
Mark Barr, an American mathematician, in about 1909, gave
the golden ratio the name of phi, the first Greek letter in the
name of Phidias, the Greek sculptor who lived around 450 BC
-
Helge von Koch (1870 to 1924) developed the snowflake curve, which is
jagged everywhere.
-
Ernst Zermelo (1871 to 1953) was a German logician and
mathematician, whose work has major implications for the
foundations of mathematics. He is known for his role in
developing Zermelo-Fraenkel axiomatic set theory and his
proof of the well-ordering theorem, which originally
involved use of the 'Axiom of Choice'.
-
Bertrand Russell (1872 to 1970) - Russell's paradox threatened the
foundations of mathematics
-
Gino Loria (1862 to 1954) was an Italian mathematician
and historian of mathematics. Loria did research on
projective geometry, special curves and rational
transformations in algebraic geometry, and elliptic functions.
He is best known as a historian of mathematics. He wrote a
history of mathematics and was especially concerned with
the history of mathematics in Italy and among the ancient Greeks.
-
Edmund Georg Hermann Landau (1877 to 1938) was a German
mathematician who worked in the fields of number theory and
complex analysis. In 1903, Landau gave a much simpler proof
than was then known of the prime number theorem and later
presented the first systematic treatment of analytic number
theory in the 'Handbuch der Lehre von der Verteilung der
Primzahlen'.
-
Albert Einstein (1879 to 1955) - 'nuf said.
-
Oswald Veblen (1880 to 1960) was an American
mathematician, geometer and topologist, whose work
found application in atomic physics and the theory of
relativity. He proved the Jordan curve theorem in 1905.
The Jordan Curve Theorem states that a continuous
closed curve cuts the plane into two distinct parts. There
are so many 'pathological' curves, such as the snowflake
curve and space-filling curves, that a complete proof is
very tricky.
-
Lipot Fejer (1880 to 1959) was a Hungarian mathematician.
In 1911, Fejér was appointed to the chair of mathematics
at the University of Budapest and he held that post until
his death. He was the thesis advisor of mathematicians
such as John von Neumann, Paul Erdos, George Pólya and
Pál Turán. Fejér's research concentrated on harmonic
analysis and, in particular, Fourier series. Fejér
collaborated to produce important papers, such as
a major work with Frigyes Riesz in 1922 on conformal
mappings (specifically, a short proof of the Riemann
mapping theorem).
-
Liutzen (L.E.J.) Brouwer (1881 to 1966) was a Dutch
mathematician and philosopher, a graduate of the
University of Amsterdam, who worked in topology, set theory,
measure theory and complex analysis. He worked with
fixed point theorems - in particular, the 'hairy ball theorem'
- if every point on a sphere is assigned a direction along
the sphere, there will be at least one point with no direction.
-
Emmy Noether (1882 to 1935) was an influential German
mathematician known for her groundbreaking contributions
to abstract algebra and theoretical physics. Described
by Pavel Alexandrov, Albert Einstein, Jean Dieudonné,
Hermann Weyl, Norbert Wiener and others as the most
important woman in the history of mathematics, she
revolutionized the theories of rings, fields, and algebras.
In physics, Noether's theorem explains the fundamental
connection between symmetry and conservation laws.
-
Tobias Dantzig (1884 to 1956) was a Baltic German
Russian American mathematician and the author of 'Number:
The Language of Science - A critical survey written for the
cultured non-mathematician' (1930) and 'Aspects of Science'
(1937).
-
George Polya (1887 to 1985) - Hungarian - emigrated to the U.S. in 1940 -
In mathematics education, wrote a set of principles for solving mathematical
(and other) problems - published in 'How to Solve It' (1957).
-
Aleksandr Friedmann (1888 to 1925) was a Russian and
Soviet physicist and mathematician. He is best known for
his pioneering theory that the universe is expanding,
governed by a set of equations he developed now known as
the Friedmann equations.
-
Abraham Frankel (1891 to 1965) - set theory - Zermelo and Frankel
put set theory on a secure axiomatic foundation, clarifying what is a set
and what is not.
-
Stefan Banach (1892 to 1945) - Given three solids, there is a plane
cutting each of the three solids exactly in half. A later, more general
result is called the Stone-Tukey theorem, which states:
Given n shapes in n-dimensional space, there is an (n - 1) dimensional plane
that cuts each of the shapes in half.
Because there can be very 'hairy' shapes, this proof can be expected to be
difficult --- like the Jordan Curve Theorem (see Osvald Veblen).
-
Mauritz Cornelius Escher (1898 to 1972) was a Dutch
graphic artist. He is known for his often mathematically
inspired woodcuts, lithographs, and mezzotints. These
feature impossible constructions, explorations of infinity,
architecture, and tessellations.
-
Dietrich Mahnke (1884 to 1939) was a German philosopher
and historian of mathematics. Mahnke's work in the history
of mathematics focussed primarily on Leibniz's development
of the infinitesimal calculus. At the time of his death,
Mahnke was editing of volume of Leibniz's mathematical
correspondence. This project was then taken over by
Joseph Ehrenfried Hofmann. Mahnke was killed in a car accident.
-
Karl Menger (1902 to 1985) was an American mathematician.
He is credited with
Menger's theorem. He worked on mathematics of algebras,
algebra of geometries, curve and dimension theory, etc.
Moreover, he contributed to game theory and social sciences.
He has been associated with
'the traveling salesman problem' :
A traveling salesman must visit a number of cities. What is
the most efficient route?
-
Oskar Morgenstern (1902 to 1977) was a German-born
economist. In collaboration with mathematician John
von Neumann, he founded the mathematical field of
'game theory' and its application to economics.
-
John von Neumann (1903 to 1957) was a Hungarian pure
and applied mathematician. He made contributions in many
areas of mathematics and physics, including game theory.
He worked on the Manhattan project, which
was set up in 1942 to develop atomic bombs.
-
George Stibitz (1904 to 1995), a Bell Labs researcher,
in 1937 built a machine, on his kitchen table,
that did binary arithmetic. He is known for his work in
the 1930s and 1940s on the realization of Boolean logic
digital circuits using electromechanical relays as the
switching element. (See Claude Shannon, below.)
-
George Gamow (1904 to 1968) was a theoretical physicist
and cosmologist - notably an early advocate and developer
of Lemaître's Big Bang theory. He discovered a theoretical
explanation of alpha decay via quantum tunneling, and
worked on radioactive decay of the atomic nucleus,
star formation, stellar nucleosynthesis and Big Bang
nucleosynthesis (which he collectively called
nucleocosmogenesis), and molecular genetics. In his middle
and late career, Gamow focused more on teaching, and
became well known as an author of popular books on science,
including 'One Two Three ... Infinity'.
-
Marian Rejewski (1905 to 1980) a Polish mathematician who succedded in
breaking the basic Enigma code of the Germans near the start of world war II.
-
Tommy Flowers (1905 to 1998), a telecommunications and electronics expert,
using his experience of the British telephone system, proposed the 'Colossus'
electronic computer for decoding top-secret German messages.
-
Albert W. Tucker (1905 to 1995) dealt with the prisoner's dilemma, the most famous
example in game theory: Two suspects are arrested. Should each one stay silent
or confess to the crime?
-
Alexandr Osipovich Gelfond (1906 to 1968) was a Soviet
mathematician. His most famous result is the Gelfond theorem:
If alpha and beta are algebraic numbers (with alpha not equal
0 or 1), and if beta is not a real rational number, then any
value of alpha-to-the-beta is a transcendental number.
Before Gelfond's work, only a few numbers such as e and pi
were known to be transcendental. After his work, an infinite
number of transcendentals could be easily obtained. Some of
them are named in Gelfond's honor: 2^sqrt(2) is known as
the Gelfond-Schneider constant, and e^pi is known as
Gelfond's constant.
-
Kurt Godel (1906 to 1978) showed the 'consistency' of 'the
Continuum Hypothesis' --- the hypothesis that there is no
infinity between the infinities of natural and real numbers.
That is, he showed you cannot disprove it. (See Paul Cohen.)
-
John Mauchly (1907 to 1980) helped develop ENIAC, the first, general-purpose
electronic computer. (See Eckert below.)
-
Alan Turing (1912 to 1954) described machines that define what is
and what is not possible in terms of computing. He built on what Rejewski
had done to break the Enigma code of the Germans on a daily basis, as the
code was changed each day, during world war II.
-
Paul Erdos (1913 to 1996) wrote an astonishing number of mathematical
papers (1,500), wandering from country to country with only a suitcase,
collaborating with other mathematicians.
The Erdos number is named after him. It is a measure of collaboration with Erdos.
1 means direct collaboration. The smaller the Erdos number of a mathematical
collaborator, the more closely the collaborator is connected with Erdos.
-
Claude Shannon (1916 to 2001) in 1937 showed how to design circuits
for binary arithmetic.
-
Charles Frederick Mosteller (1916 to 2006) was one of
the most eminent statisticians of the 20th century. He was
the founding chairman of Harvard's statistics department,
from 1957 to 1971. Mosteller wrote over 50 books and over
350 papers, with over 200 coauthors. He was an avid fan of
the Boston Red Sox and attended the games in the run up
to the World Series. He conducted perhaps the first academic
investigation of baseball after his favorite team, the
Boston Red Sox, lost the 1946 World Series. He has been
mentioned with 'the Secretary Problem' - choosing the
best secretary from a pool of candidates.
-
Edward Norton Lorentz (1917 to 2008) was an American
mathematician and meteorologist, and a pioneer of chaos
theory. He discovered the strange attractor notion and
coined the term 'butterfly effect'.
-
J. Presper Eckert (1919 to 1995) helped develop ENIAC, the first, general-purpose
electronic computer. (See Mauchly above.)
-
Rene Thom (1923 to 2002) - Catastrophe theory deals with slight changes
that can lead to great changes. Thom sought to find a mathematical way
to analyze catastrophic changes.
-
Benoit Mandelbrot (1924 to 2010) did work on fractals.
-
Wolfgang Haken (1928 to ?), with Kenneth Appel, proved the 4 Color Conjecture
--- with the help of about 1,200 hours on a computer.
-
Kenneth Appel (1932 to 2013), with Wolfgang Haken, proved the 4 Color Conjecture
--- with the help of about 1,200 hours on a computer.
-
Roger Penrose (1931 to ?), an English physicist, invented several
'tesselations' of the plane, built up from two quadrilaterals known
as 'kites' and 'darts', due to the shape of those quadrilaterals.
These tesselations are not periodic: they do not repeat themselves
and any two parts of the tesselation are essentially different from
each other.
-
Paul Cohen (1934 to 2007) showed the 'independence' of 'the
Continuum Hypothesis' --- the hypothesis that there is no infinity
between the infinities of natural and real numbers. That is, he showed
the continuum hypothesis is undecidable --- it can be neither proved
nor disproved from the standard ZF (Zermelo-Fraenkel) axioms.
(See Kurt Godel above.)
-
Robert May (1938 to ?) is an Australian scientist who studied
chemical engineering and theoretical physics (B.Sc. 1956) and
received a Ph.D. in theoretical physics in 1959. He has provided
a model for population growth that takes limited resources into account.
Reference: His 1976 paper "Simple mathematical models with very
complicated dynamics".
-
John Horton Conway (1937 to ?) is a British mathematician
active in the theory of finite groups, knot theory, number theory,
combinatorial game theory and coding theory. He has also contributed
to many branches of recreational mathematics, notably the invention
of the cellular automaton called 'the Game of Life', which has been
implemented as a computer program.
-
Yuri Matiyasevich (1947 to ?) showed that if there is a rule for finding
the elements of a set, the search for the elements can be carried out by
an algebraic formula
--- and no matter how complicated the rules are for listing the terms, the
rules can be expressed just in therms of +, -, and x. In short, every recursively
enumerable set is Diophantine.
In the 17th century two formulae were suggested for listing primes: 2^n - 1 and
2^2^n + 1. In fact, the primes are a recursively enumerable set. Just look at each
number in turn and if it is a prime, write it down in the list.
Matiyasevich realized that there must be a Diophantine formula for listing the
primes but he thought it would be too complicated to write down. But J. P. Jones
found such a formula in 1976. See J.P. Jones.
-
James P. Jones ( ? to ?) in 1976 found a formula to list the primes. This
used 26 variables, which was very convenient, otherwise he would have had
to extend the alphabet. See page 195 of 'The Little Book of Mathematical Principles'
mentioned in the Introduction at the top of this page.
-
Stephen Cook (1939 to ?) - If P = NP were shown to be true, the
secrecy of codes (encryption) would be under threat. P = Polynomial ;
NP = Near Polynomial. P = NP means if a problem is 'tractable' with a lucky
guess (NP), then it is tractable without such a guess (P).
-
Andrew Wiles (1953 to ?) proved Fermat's conjecture that there are no
solutions in positive integers of x^n + y^n = z^n, if n is larger than 2.
x=3, y=4, z=5 is a solution for the case when n=2.
The case for n=3 was proved in 1770 --- for n=5 in 1825 --- for n=7 in
1839. (Only prime number need to be considered.) Then all cases up to
n=100 were proved, but no 'complete' solution was found until 1994.
-
Thomas C. Hales (1958 to ?) provided a proof of the conjecture on the
most efficient way to stack spheres (which is the way grocers stack their
oranges). Hale's proof was so complicated that it could not be done by hand.
Like the 4 Color Conjecture, it needed very many cases to be checked by a
computer, and so, as with the 4 Color proof, it has been reluctantly accepted
by mathematicians.