|
INTRODUCTION :
In 2016 I started trying to wade through the 'Principia' (full name
'Philosophiae Naturalis Principia Mathematica') of
Isaac Newton.
I bought the
English translation of the 3rd (1726) version of the 'Principia'
as translated into English by Bernard Cohen and Anne Whitman (with help
from Julia Budenz), 1999, University of California Press. (I got the
version without Cohen's 'Guide'.)
I found that this is a tough slog (as many others in the 1600's and 1700's
found it to be), so I bought the book
Magnificent Principia by Colin Pask.
By reading in bits and pieces ('baby steps') from both Cohen-Whitman and Pask,
I found I could gradually absorb more and more of what the amazing man deduced
and 'synthesized'.
As Pask points out (on page 167 of his book):
"There is no doubt that dressing up ideas from calculus in geometrical form
made it virtually impossible for many to read the Principia."
Furthermore, Pask quotes William Whewell from his 1837 'History of the Inductive
Sciences":
"... we gaze at it [the Principia] with admiring curiosity, as on some gigantic
implement of war, which stands idle among the memorials of ancient days, and
makes us wonder what manner of man he was who could wield as a weapon what we can
hardly lift as a burden."
On the other hand, Pask occasionally points out, as on page 184 of his book
'Magnificent Principia':
"I suspect that in retrospect, many people will feel that [in some steps], Newton
exhibited the physics of ... motion better than we see it through [today's
vector-calculus equations]."
Pask leaves many of Newton's propositions/theorems/corollaries/lemmas
undiscussed. I find that I may find answers to many of my questions by
looking at still other authors who have tried to make Newton's writings
understandable to a wider audience.
Many books on Newton have nary a geometric diagram and nary an algebraic expression
in them --- no mentions of ratios and 'ultimate ratios'. Those are not books
that will help me.
However, in some university libriaries, I have found some books that I may
eventually buy for further reading in bits and pieces (more baby steps).
Namely:
Chandrasekhar works his way through almost all the propositions and corollaries
of the Principia. De Gandt takes an approach that might be more digestable
for many readers --- an approach that may be a good introduction to the more
exhaustive approach of Chandrasekhar.
A few years before the first edition of the 'Principia' was published in 1687,
Newton wrote a smaller work (about 9 pages), titled 'De motu corporum in gyrum'
(On the motion of bodies in an orbit). De Gandt (in French) essentially provides
an explanation of 'De motu'.
For more information, here are some 'general web searches'
on these authors and titles:
Newtonian scholars who are not afraid to show some
mathematics in their works on Newton include
To give an idea of why it is important that many people on this
earth should understand something of the contributions of Newton
to the body of human knowledge, here are several quotes
from Einstein:
-
"The whole evolution of our ideas about the processes
of nature, with which we have been concerned so far,
might be regarded as an organic development of Newton's
ideas."
-
"We have to realize that before Newton, there existed no
self-contained system of physical causality which
was somehow capable of representing any of the deeper
features of the empirical world."
-
In 1927, on the 200th anniversary of the death of Isaac Newton,
Einstein wrote: "we feel impelled at such a moment to remember
this brilliant genius, who determined the course of western
thought, research, and practice like no one else
before or since."
MY MOTIVATION:
After I retired (in 2005) --- and, in particular, after 2009 (when I
switched from Microsoft operating systems to Linux on my desktop and
laptop computers), I started on a retirement hobby of developing
software in the
Tcl-Tk programming language.
Many of the programming projects that I put on my 'to-do' list
involved bringing many of the classical mathematical results
(theorems) of Thales, Euclid, Archimedes, Newton, Euler, etc.
'to life' --- via animated or interactive presentation
of the mathematical results (geometry, number theory, sequences,
series, fractals, whatever) on a 'Tk canvas'.
The 'Newton-math' books (and other sources) on this page are meant
to help give me ideas for 'classical mechanics' projects to undertake
--- in particular, 'integration of ordinary differential equations'
--- with depiction of motions on a Tk 'canvas'.
To augment the lists of links on this page, I have a
a page of math PDF's --- mostly public domain documents
gathered from the
gutenberg.org site --- or from the
archive.org site.
Also, I have
a page of mathematician names, in chronological order (a 'timeline' of
mathematicians) --- with links to more information on each mathematician.
For my software projects, I have bought many math and math-physics books.
Many of my 'hard-copies' are listed on a
'math book inventory' page. (This page is probably way out of date,
because I am continually adding to my collection/inventory, without
updating that page.)
If the lists on this page and the other pages of this site do not satisfy
my need for more software projects, I may wish to scan the
list of physicists at Wikipedia.
In addition, here is a page of
physics-related lists at Wikipedia.
And here is a
list of mathematicians at Wikipedia.
In particular, here is a page for
mathematicians by nationality, and here is a page for
mathematicians by century.
More mathematicians (and physicists) can be found via the
Galileo Project of Rice University. A convenient list of
many of those mathematicians' names on one page (including
Kepler and Newton) is
here.
This
Should I become a mathematician? thread at physicsforums.com
provides many interesting source books on mathematics and mathematicians.
A few more books with the intent of popularizing math (i.e. taking
math to the masses) can be found at the Wikipedia pages on
Popular_mathematics and
Recreational_mathematics.
THE NEWTON-INFO SOURCE-LINKS BELOW
The book titles (and some of the author names) will usually be a link
to more information on the book (and author). Often, the book-title link will be to
amazon.com (for reader reviews, in particular) --- and the author
link may be to
Wikipedia.
Alternatively, the book-title link may be to a site like Google Books,
which may have some excerpts from the book --- and the author link
may be to the author's web site.
In the first releases of this page, many of the links to journals
and magazines may be 'general web searches', not links to the website
of the journal or magazine. This is because many of these sites
only offer their articles for a fee. I see their need to cover their
costs, but, in order to support
STEM programs, it would be nice
if they would put their old publications in the public domain ---
say articles more than 20 years old --- or articles by people
who are no longer alive --- or articles by people (or their legal survivors)
who have released their articles under a
'Creative Commons' license.
SEARCHING THIS PAGE :
If you are looking for some particular information, you can use
the text search function of your web browser.
For example, if you are looking for information on a
topic such as 'geometry', 'calculus', or 'trigonometry',
enter a key-string such as 'geom', 'calc', or 'trig'
in the text search entry field of your web browser.
THE WONDERMENT OF IT ALL :
The wheels of thought that Newton set into motion offer many occasions for
wonderment at the logical and geometric beauties of mathematical-physics
subject matter.
Kepler said (ref: page 55 of Pask's book):
"Astronomers should not be granted excessive licence to conceive
anything they please without reason: on the contrary, it is also
necessary for you to establish the probable causes of your Hypotheses
which you recommend as the true causes of Appearances. Hence, you must
first establish the principles of your Astronomy in a higher science,
namely Physics or Metaphysics."
And:
"My goal is to show that the heavenly machine is not a kind of divine
living being but similar to a clockwork insofar as almost all the manifold
motions are taken care of by one single absolutely simple magnetic bodily
force, as in a clockwork all motion is taken care of by a simple weight.
And indeed I also show how this physical representation can be presented
by calculation and geometrically."
Newton responded to this challenge and took Kepler's laws many steps further.
Newton must have felt that he went a long way toward the goal he laid out
for himself (ref: page 92 of Pask's book):
"... the difficulty of philosophy [what we call today 'physics']
seems to consist in this --- from the phenomena of motions to investigate
the forces of nature, and then from these forces to demonstrate the other phenomena."
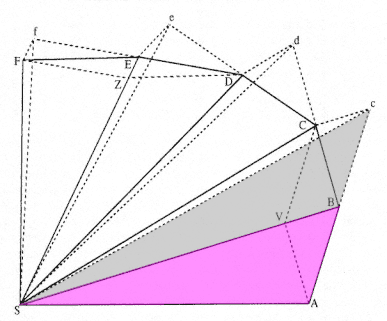
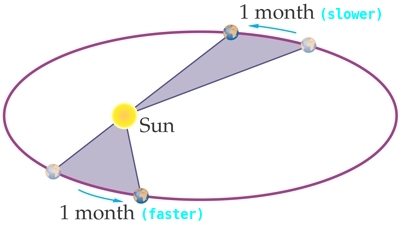
Newton demonstrated that an inverse-square 'law' of gravitational attraction
explained elliptic (and parabolic and hyperbolic) planetary/celestial orbits.
And he went on to show how that same 'law' could explain many phenomena:
-
motions of moons
(of Earth and Jupiter and Saturn)
-
motions of pendulums
(at various altitudes)
-
motions of projectiles and pendulums
(taking into account air/fluid resistance)
-
the phenomena of tides
(mainly due to lunar and solar gravity)
-
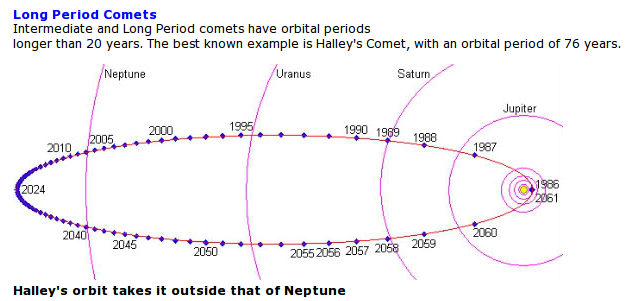
motions of comets
(predicting the month of their return)
-
for more, see his 'Book III'.
Newton did not 'feign a hypothesis' to explain the cause of gravity.
Like Kepler, he had considered magnetic or electrical causes, but
could not resolve the issues that arose.
Even physicists today (2016) are struggling with that problem.
Although he could not answer all the questions that he raised,
it is no wonder that England buried him as if he were a military hero.
(Voltaire was impressed with the funeral.)
I look forward to following in the footsteps of his thoughts.
|